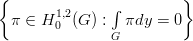Abstracts of some lectures
For the complete list of lectures see schedule.Miloslav Feistauer
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
feist@karlin.mff.cuni.cz
Analysis of the space-time discontinuous Galerkin method for the numerical solution of nonstationary nonlinear convection-diffusion problems
The paper presents the theory of the discontinuous Galerkin finite element method for the space-time discretization of a nonlinear nonstationary convection-diffusion initial-boundary value problem. The discontinuous Galerkin method is applied separately in space and time using, in general, different space grids on different time levels and different polynomial degrees p and q in space and time dicretization. In the space discretization the nonsymmetric, symmetric and incomplete interior and boundary penalty (NIPG, SIPG, IIPG) approximation of diffusion terms is used. The paper is concerned with the proof of error estimates in “L2(L2)”- and “DG”-norm formed by the “L2(H1)”-seminorm and penalty terms. Special space-time interpolation and a special technique has been applied for obtaining optimal error estimates with respect to the time step.
Jan Franců
Faculty of Mechanical Engineering, Brno University of Technology, Czech Republic
francu@fme.vutbr.cz
On two-scale convergence
Homogenization is a mathematical method developed for modelling media with periodic structure. In mathematic setting it studies behavior and the limit of solutions to the sequence of differential equations e.g. -∇(an ·∇ un)=f with periodic coefficients an(x) when its period εn tends to zero.
The key point of the homogenization theory is passing to the limit in the product of two weakly converging sequences {an} and {∇ un}. The problem is solved by a special convergence called two-scale convergence introduced by G. Nguetseng and Allaire. The adjoint approach to the two-scale convergence by D. Cioranescu, A. Damlamian, G. Griso is based on periodic unfolding. The contribution deals with its modification which removes some problems and simplifies the proofs.
Giovanni P. Galdi
Department of Mechanical Engineering and Materials Science,
Department of Mathematics, University of Pittsburgh, U.S.A
galdi@pitt.edu
Steady-State Navier-Stokes Flows Past a Rotating Body: Leray Solutions are Physically Reasonable
Consider a body, B, moving by an arbitrarily prescribed rigid motion, with translational and angular velocity ξ and ω, respectively, in a Navier-Stokes liquid, L, that fills the whole space exterior to B. As is well-known, it is convenient to refer the motion of L to a frame, S, attached to B. We are interested in steady-state flow of Lin S, which requires that ξ and ω, when referred to S are constant vectors.
It is a classical result that the exterior Navier-Stokes boundary-value problem associated with this type of flow has a "weak" solution, that is, the velocity field v has a finite Dirichlet integral, for data of arbitrary size (Leray solution). Recently, in a joint work with Ana L. Silvestre, the author has shown that, if the data are "small in size", then the problem admits a Physically Reasonable (PR) solution according to R. Finn, that is, it satisfies the equation of energy balance, shows a "wake" behind the body (provided I := ξ · ω ≠ 0), and it is stable in the sense of Liapounov.
It is easily established that a PR solution is also Leray, but the converse is far from trivial, even for small data.
The main objective of this talk is to show that, if I ≠ 0, a Leray solution is also Physically Reasonable for data of arbitrary size. We shall also analyze several interesting consequences of this result, including the geometric structure of the solution set.
Tomáš Roubíček
Mathematical Institute of Charles University, Prague, Czech Republic
roubicek@karlin.mff.cuni.cz
Approximation techniques in rate-independent processes
The quasistatic initial-value problem for systems governed by doubly nonlinear variational inequality involving (possibly nonconvex) stored-energy and a degree-1 homogeneous dissipation-energy functional will be adressed. The modern concept of the so-called energetic solution will be presented together with time-discretisation and space-approximation techniques that leads to numerical schemes with guaranteed convergence and efficient algorithms. The theory will be accompanied by illustrations on some specific applications in inelastic processes in continuum mechanics of solids, like plasticity, damage, delamination, or phase transformations.
Adélia Sequeira
Department of Mathematics and CEMAT, Instituto Superior Técnico, Lisbon, Portugal
adelia.sequeira@math.ist.utl.pt
The geometrical multiscale modelling in hemodynamics
Mathematical modeling and numerical simulation can provide an invaluable tool for the interpretation and analysis of the circulatory system functionality, in both physiological and pathological situations. However, although many substantial achievements have been made, most of the difficulties are still on the ground and represent major challenges for the coming years.
In this talk we introduce some basic differential models for the description of blood flow in the circulatory system. We extend to a generalized Newtonian shear-thinning blood flow model, existing results for 3D FSI problems with Newtonian fluids, using a fully implicit coupled algorithm. We discuss the geometrical multiscale approach to simulate the reciprocal interactions between local and systemic hemodynamics. It consists in coupling a hierarchy of models with different levels of complexity, namely 3D FSI models, 1D hyperbolic and 0D or lumped parameter models. The effectiveness of the couplings and the geometrical multiscale strategy is illustrated through numerical simulations.
Christian G. Simader
Department of Mathematics, University of Bayreuth, Germany
christian.simader@uni-bayreuth.de
A Stokes-like system of fourth order
In a bounded domain G ⊂ ℝ
(n ≥ 2) we study weak solutions u
∈ H02,2(G) = (H02,2(G))n,
p ∈ H0,01,2(G) =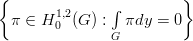 
for given F* ∈
H02,2(G)*
of the system
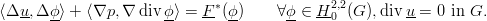
In addition a Lq-theory (1 < q < ∞) holds true. Similar to Stokes’ system a Cosserat operator exists with analogous regularity properties.
Vladimír Souček
Mathematical Institute of Charles University, Prague, Czech Republic
soucek@karlin.mff.cuni.cz
On a prolongation of a class of overdetermined semi-linear systems of PDE's
In 60's, D. C. Spencer studied in detail properties of overdetermined linear systems of PDE's. Later on, Bernstein, Gel'fand and Gel'fand, resp. Lepowsky, developed a theory of (generalized) Verma modules for simple Lie algebras and their homomorphisms, and they found in such a way a construction of resolutions for a wide class of overdetermined linear systems (possibly of higher order), invariant with respect to a chosen simple Lie algebra. The most interesting particular case of this situation consists of an infinite family of conformally invariant systems of PDE's. In the lecture, I will describe a recent approach to such linear overdetermined systems, their semi-linear versions and their prolongations.
Wolfgang L. Wendland
Institute for Applied Analysis and Numerical Simulation, University of Stuttgart, Germany
wendland@mathematik.uni-stuttgart.de
On boundary integral equations for two–dimensional slow viscous flow past a porous body
In this lecture, we use the method of matched asymptotic expansions for the two-dimensional steady flow of a viscous incompressible fluid at low Reynolds number past a porous body of arbitrary shape. We assume that the flow inside the porous body is described by the Brinkman model, i.e., by the continuity and Brinkman equations, and that the velocity and boundary traction fields are weakly continuous across the interface between the fluid and the porous medium. By employing indirect boundary integral representations, the problem is reduced to uniquely solvable systems of Fredholm integral equations of the second kind in some Sobolev or Hölder spaces. It is shown that the flow and also the force exerted by the exterior flow on the porous body admit an asymptotic expansion with respect to low Reynolds number, whose terms depend on the solutions of the above mentioned systems of boundary integral equations.
By using the Oseen flow in the exterior, it can be shown that the Stokes–Brinkman expansion converges in any compact region to the Oseen–Brinkman solution if the Reynolds number tends to zero, in a similar manner as shown by G.C. Hsiao and R.C. MacCamy in 1973 and 1982 for flows around rigid obstacles.
M. Kohr, G.P. Raja Sekhar, W. L. Wendland: Boundary integral equations for two–dimensional low Reynolds number flow past a porous body. Math. Methods Appl. Sci. 31 (2008) 1065–1097.