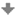Portál středoškolské matematiky
Odchylka přímek p(P, u), q(Q, v) je číslo φ ∈ <0, π/2>, pro které platí:
\(\cosφ = \dfrac{|uv|}{|u||v|}\).
Spočítejte odchylku dvou přímek p(A; u) a q(B; v), je-li A[-1; -7; -6], B[2; 1; 4], u = (-1; 3; 0) a v = (9; -6; 0).
Odchylku přímky a roviny nepočítáme přímo, ale využijeme znalostí, které již máme.
Je-li přímka p kolmá k rovině ρ, je jejich vzájemná odchylka φ = π/2.
Není-li přímka p kolmá k rovině ρ, je jejich odchylka rovna odchylce přímky p a průsečnice p' rovin ρ a ψ, kde p ∈ ψ a ρ ⊥ ψ.
Ještě jednodušší je, sestrojit kolmici q k rovině ρ a počítat odchylku α přímek p a q. Vztah mezi hledanou a získanou odchylkou je:
φ = π/2 - α.
Pro výpočet odchylky φ přímky p(A, u) a roviny ρ(B, n) můžeme použít vzorec:
\(\sinφ = \cosα = \dfrac{|un|}{|u||n|}, φ \in \langle 0°;90° \rangle\).
Spočítejte odchylku přímky p(A; u) a roviny ρ: 9x + 2y + 4 = 0, je-li A[-2; 5; -1], a u = (9; -5; 4).
Odchylka rovin ρ a ψ, je rovna odchylce přímek p a q, pro které platí p = (ρ ∩ σ), q = (ψ ∩ σ), kde σ je rovina kolmá na ρ i ψ.
Slovy bychom výše uvedenou definici mohli rozepsat takto:
Odchylku φ dvou rovin ρ a ψ, vypočítáme následujícím způsobem. Nejprve najdeme rovinu, která je k oběma kolmá
. Tato rovina protne roviny ρ a ψ v přímkách p a q. Odchylka φ rovin ρ a ψ je rovna odchylce přímek p a q.
Podobně jako když jsme hledali odchylku přímky a roviny, můžeme využít normálových vektorů rovin ρ a ψ. Na obr. 4.9 je vidět, že přímky r a s svírají úhel stejné velikosti jako p a q. Odchylku dvou rovin můžeme tedy snadno určit pomocí jejich normálových vektorů.
Pro výpočet odchylky φ dvou rovin ρ(A, nρ) a ψ(B, nψ) můžeme použít vzorec vyplývající z předchozí úvahy:
\(\cosφ = \dfrac{|n_{ρ}n_{ψ}|}{|n_{ρ}||n_{ψ}|}, φ \in \langle 0°;90° \rangle\).
